Background
The failure of columns can have catastrophic consequences. To prevent this, engineers use the concept of slenderness ratio to study the column behaviour of the column with respect to its properties, geometry and expected failure. Once they have determineted the failure mode, they can take mitigation measures to strengthen the design of the column. The most common type of failure for long columns is buckling failure. Bucking occurs when applied load on the column exceeds the buckling capacity of the column. To prevent a column from buckling, sufficient lateral support or bracing must be provided along with proper selection of cross-sectional geometry.
Slenderness ratio
The slenderness ratio is the ratio of the effective length of the column to the least radius of gyration. We define the effective length as the length of an equivalent column made of the same materials with the same capacity of loading, but with hinged ends. Similarly we consider the the radius of gyration to be where the lowest moment of inertia is. It evaluates the resistance of RC (Reinforced Concrete) column to crushing or buckling. Short and long columns concerning their radius are susceptible to crushing while thinner columns concerning their radius are susceptible to buckling. Engineers calculates the radius of gyration by dividing the effective length of the column over its minimum radius of gyration.
We use the slenderness ratio as a tool to categorize columns into short, long, or slender columns. The design of short and long column is dependent upon the material properties and column aspects. The design of slender columns depends upon slenderness.
We consider columns to be slender when the dimensions of cross-sections to the length of the column is minor. A higher slender ratio implies more tendency towards the collapse of the column under a small compression load. We must give extra attention to the slenderness effect.
There are multiple codes such as ACI 318-19 or IS 456. Engineers follow procedures and specifications of mentioned codes to calculate the slenderness ratio of homogenous elastic columns.
Mathematical definition of slenderness ratio
From the Euler formula, the slenderness ratio is inversely proportional to the radius of gyration. This means the buckling tendency is maximum when r is minimum.
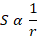
α in the above equation denotes the proportionality.
The slenderness ratio is proportional to Klu which means the greater the length greater is the buckling tendency.
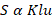
S: is slenderness ratio
K: is an effective length factor.
lu: is the unsupported length of the column.
Combining the above equations, we can calculate the slenderness ratio by the following formula.
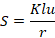
r: is the cross-sectional radius of gyration. See section Radius of Gyration below in the article for details about how to calculate it.
Free Slenderness Ratio Calculator
Following the equation above, use the calculator below to calculate the slenderness ratio of a column with unsupported length lu, effective length factor K and cross-sectional radius of gyration r.
| K: | |
| lu: | |
| r: |
| S: |
Effective length factor (K)
The value of the effective length factor varies between 0.5 -2.0 and is available in the AISC manual. Its value depends upon the attachment of the column ends to the support. A column supported at both ends follow a sine waveform when it buckles. Therefore the unsupported length is equal to effective length in that case.
Did you like this post? Sign up and we’ll send you more awesome posts like this every month.
Additionally, the effective length (Le) is the length between the point of zero moment or successive inflexion points. Zero moments is the point at which the moment becomes zero. Engineers also refer to this as the inflexion point. You can read more about this in the following article: Column buckling and why it’s important to know about
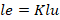
When k=1
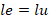
A column fixed at both ends develop a half-sine waveform when it buckles. So the effective length factor is equal to 0.5.
Perfectly fixed or perfectly hinged support conditions don’t exist in real structures. Instead they have a semi-restrained end against rotation by connecting members. In this case for laterally braced columns, K value lies in between 0.5 to 1.0.
Unsupported length (lu)
Engineers define the unsupported length as the distance between the bottom side of the slab, beam, or capital above and the top of the beam or slab below.
The unsupported length of a column can be distinct in two orthogonal directions subject to the nature of support in the respective directions.
Radius of Gyration
The geometry of the cross section dictates the the radius of gyration. A column with a low slenderness ratio and high moment of inertia is more resistant to buckling. Engineers calculates the gyration radius through the formula given below:
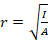
I: the moment of inertia about a centroidal axis in mm4
A: gross area of the column in mm2
Engineers use the approximate values of r=0.3h for rectangular or square section. Similarly we can use the value of r=0.25h for circular sections. The letter h in this context refers to the sectional dimension in the direction of stability we consider for the design.
Free Radius of Gyration Calculator
Following the equation above, use the calculator below to calculate the radius of gyration of a cross section r with moment of inertia I (mm4 or in4) and area of the cross section A (mm2 or in2).
| I: | |
| A: |
| r: |
ACI Criteria for Slenderness Ratio Effect
American Concrete Institute (ACI), an international body, defines the criteria for the effect of slenderness ratio. The slenderness ratio can be neglected for compression members braced against sideways when.
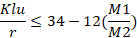
Where
M1: smaller factored end moment over compression member in N×mm.
M2: larger factored end moment over compression member in N×mm.
M1/M2: is positive for a column that is bent in double curvature.
Negative for the column that is bent in single curvature. The double curvature means that throughout the length of the column, the moment starts from point zero at the top, then at the middle it becomes zero again, and then till the end, the moment enters in negative region and end at zero value again.
Conclusion
We use columns to transfer loads from one floor to another. The slenderness ratio defines the failure mode of the column based on the effective length and the radius of gyration. It is important to know the total loads that the column has to support. To accurately calculate the loads acting on the structure, Tribby3d provides a complete solution at one stop. A convenient and easy use cloud-based software that enables the structural engineers to design and simulate the structural abilities and behaviour before finalizing the design.
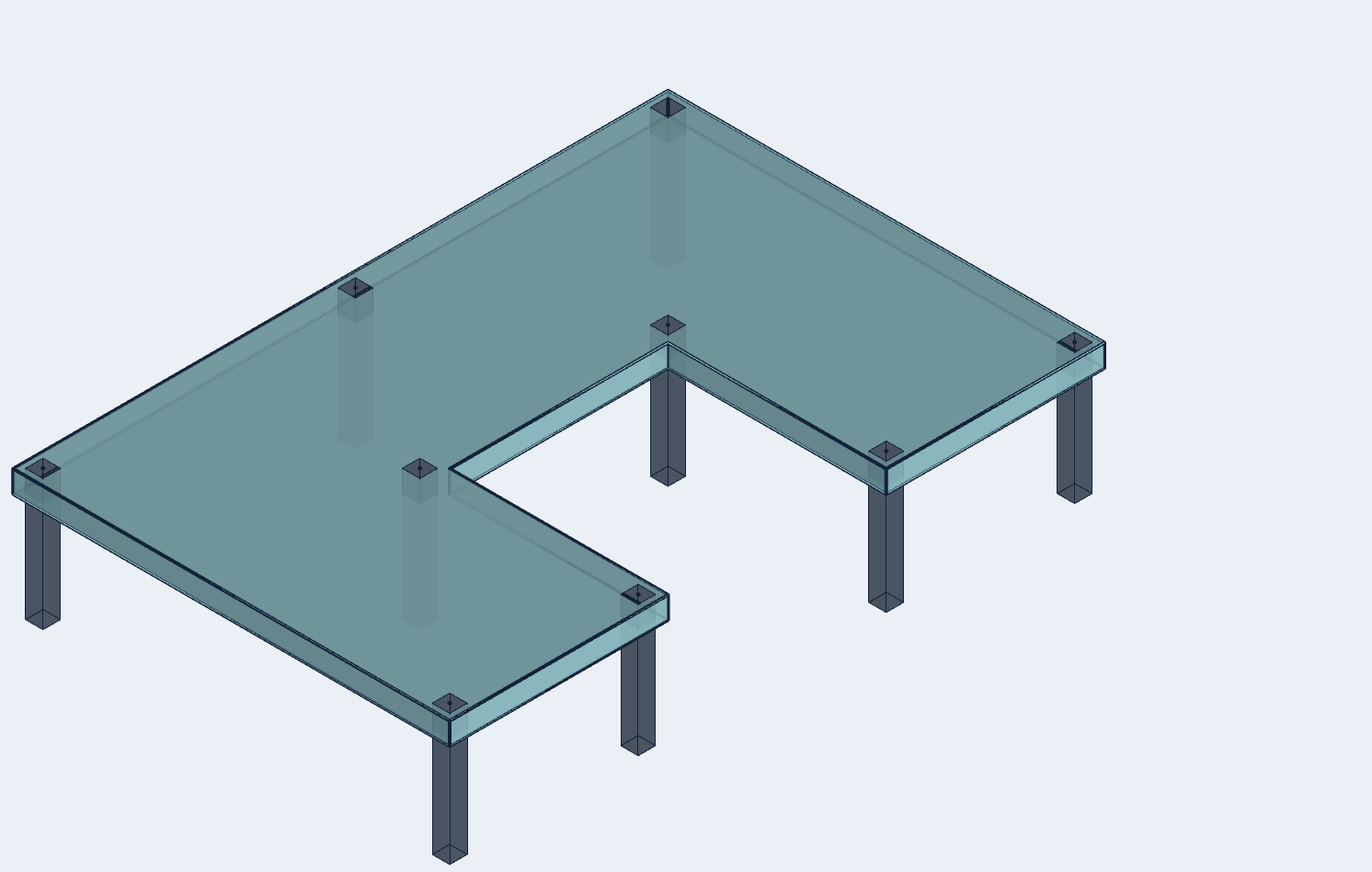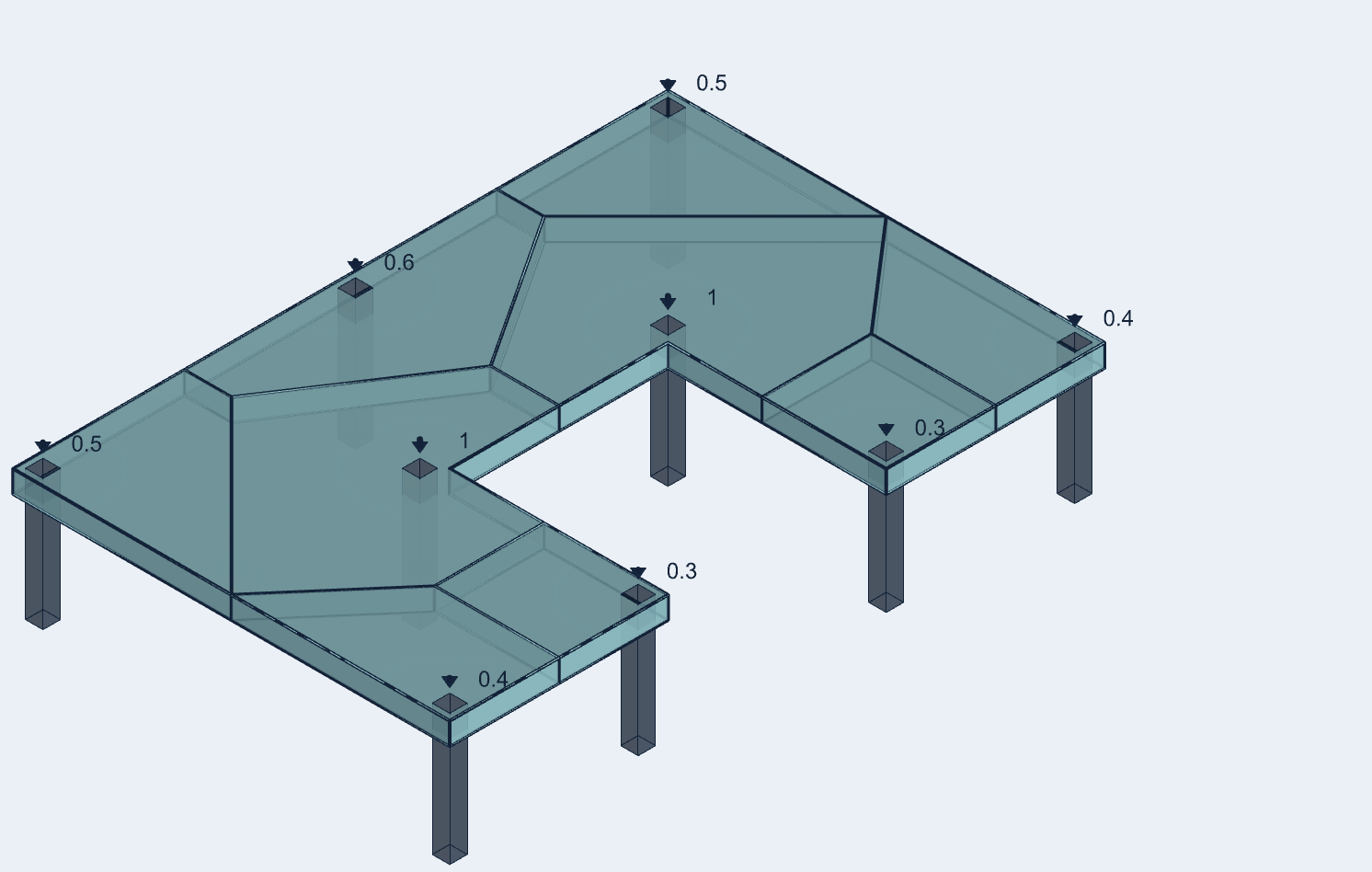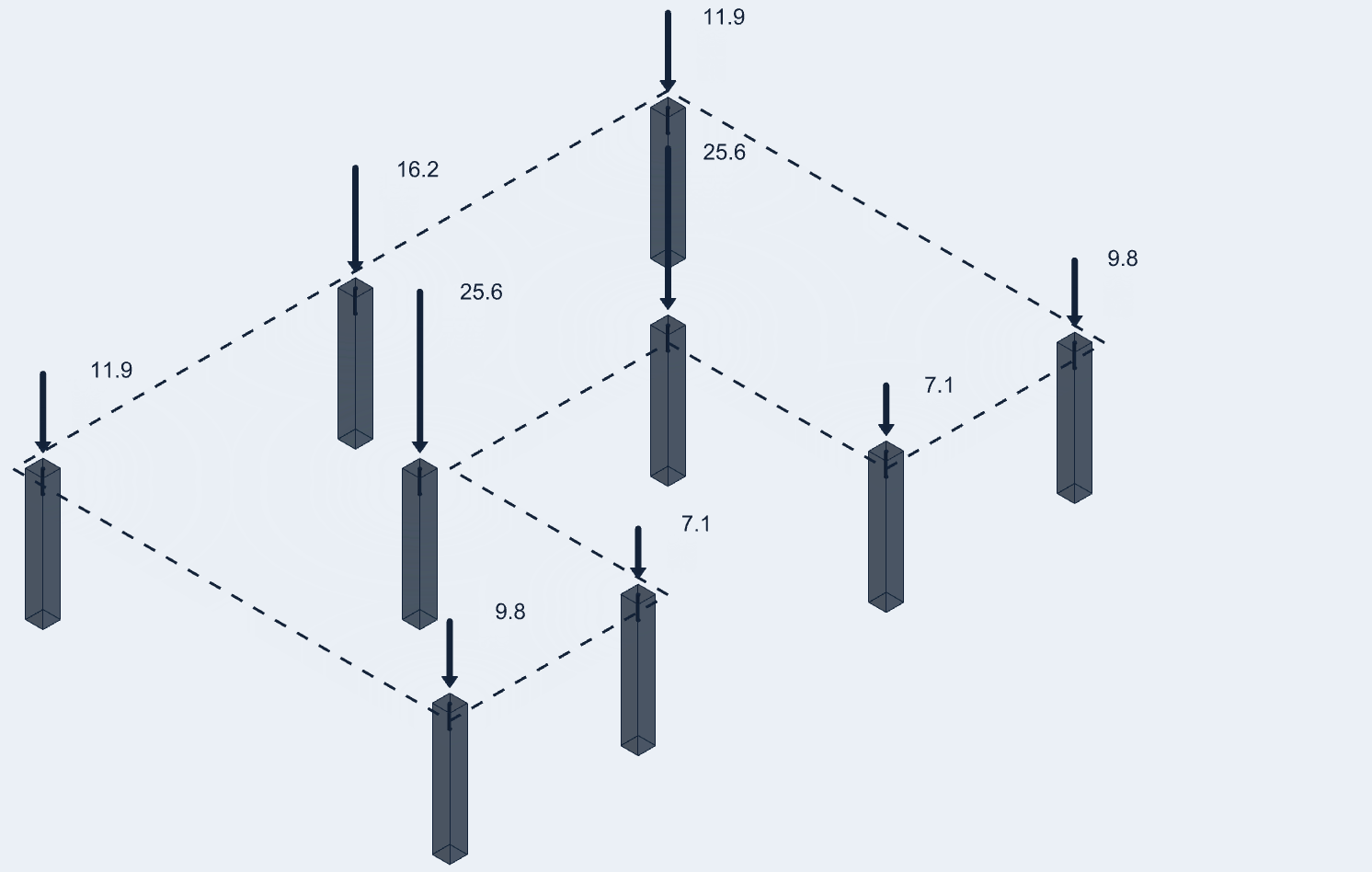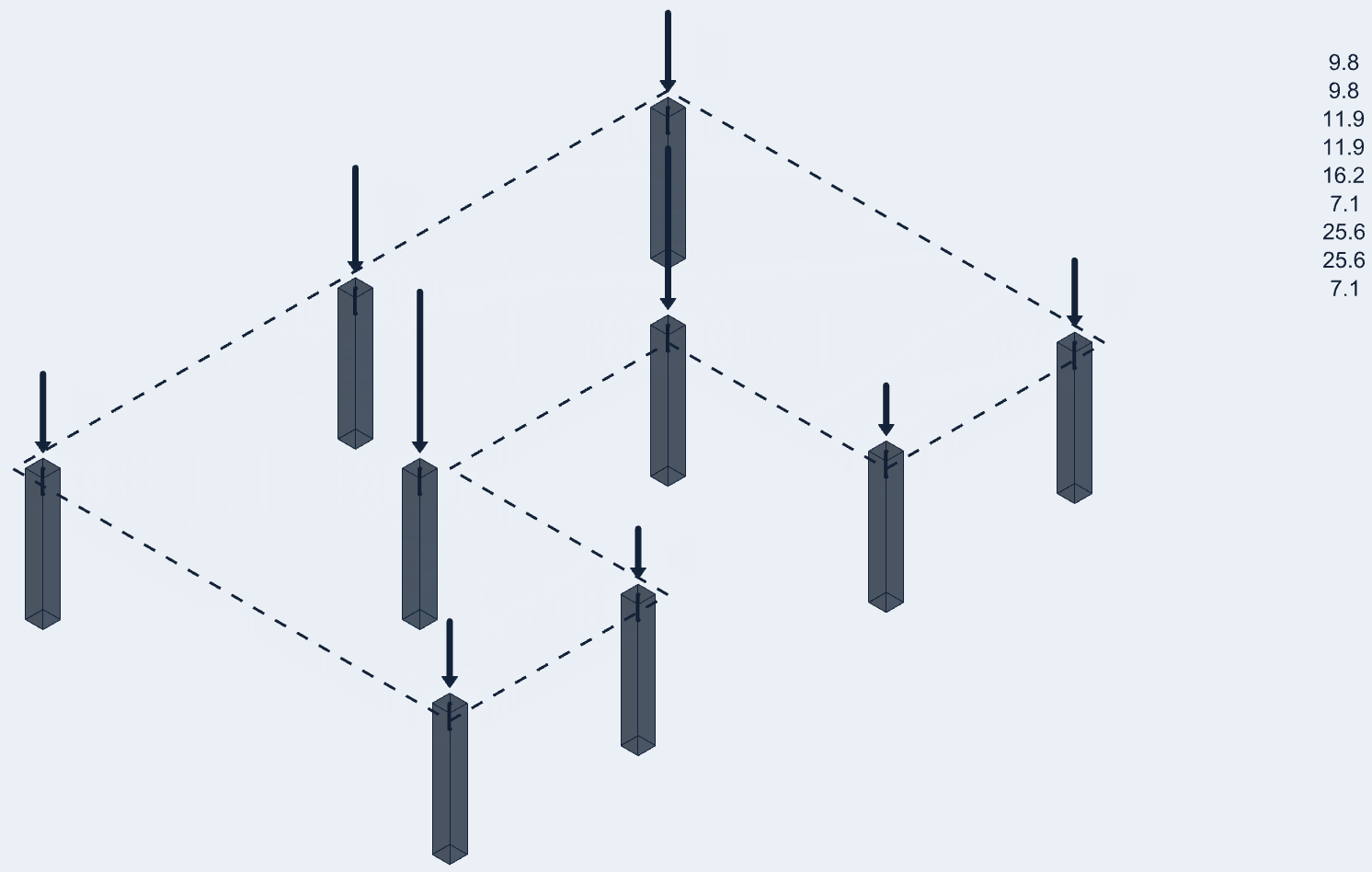
To request free access to the beta version of Tribby3d, please use this application form: Sign up
FAQ
The slenderness ratio is defined as the ratio between the effective length of the column to the least gyration radius.
A column with a slenderness ratio less than 12 is called a short column.
A column with a slenderness ratio higher than 12 is called a long column.
The effective length (Le) is defined as the length between the point of zero moment or successive inflexion points.
The slenderness ratio enables us to find the design load, help us categorize different columns and clue of buckling collapse. The higher the slenderness ratio higher is the chance of bucking failure in that direction.
The bending of the column under the axial compression force that precedes to deformation of the column is called buckling of a column.
