There are different factors that affect the stability of buildings. One of them is column buckling. This article focuses on what it is and why it’s important to consider in structural engineering. We will cover design considerations and associated equations as well.
How to calculate column loads?
Previously we have covered topics on how to caluclate column loads from floors in the two articles Tributary areas of columns and how to best calculate them and Irregular Tributary Areas and How To Best Calculate Them. Given the load on the column, the next natural step is to ensure that the resulting load does not exceed the column’s structural capacity, including column buckling.
What is Column Buckling?
Column buckling is a phenomenon in structural engineering which occurs when slender elements under high compression suddenly collapse. Thankfully design measures can be taken to prevent this. Buckling load analysis shows the maximum load that the column can resist before buckling. The factors which impact this analysis are element length, stiffness in geometry and elasticity of the material. Another important nature of the failure mode is that it is instantaneous. This is also the reason why it is so deceptive and dangerous.
Elastic Buckling
Slender columns have higher risk of experiencing elastic buckling. You can think of it as the breakage that occurs when bending a spaghetti noodle. Further more, it occurs at a level of stress that is less than the ultimate stress capacity of the material. It is due to instability in the column which results in failure.
The ideal column to resist buckling is the one that has homogenous cross-section and that it is initially straight. However, there are small imperfections in the structural elements related to fabrication and material. Buckling in columns can also be an effect of eccentric load.
Critical Load in Column Buckling
An important concept in the context is the critical load. It is the maximum compressive load in the axial direction which the column can resist before collapsing due to buckling. We can use the formula given below to calculate the critical load:
Pcr = π2E I / (K L)2
Where
Pcr , is the critical force at which the column will buckle.
E, Young’s modulus of the material,
I, Second moment of area of the cross section
K, The effective length factor
L, Unsupported length of the column
Did you like this post? Sign up and we’ll send you more awesome posts like this every month.
Free Critical Load Calculator
Given the equation above, use the calculator below to calculate the critical force Pr (N or lb), given the properties E (Pa or psi), I (m4 or in4), K (-), and L (m or in) of the column. Use either metric or imperial units – don’t mix.
| E: | |
| I: | |
| K: | |
| L: |
| Pcr: |
Calculation of Column Buckling
In addition to the equation above, Euler’s formula provides an appropriate equation to calculate the critical stress. We will discuss Euler’s formula along with other important factors in further discussion.
σcr = π2E/ ( Le/ r)2
Where,
σcr , Critical stress which is basically the average stress at which the column buckles.
L, Unsupported length of the column.
A, The cross-sectional area of the column.
E, The elastic modulus of the material.
K The factor of length. It shows the end condition of the column. In the next section, this blog will discuss the effective length factor.
Column End Conditions
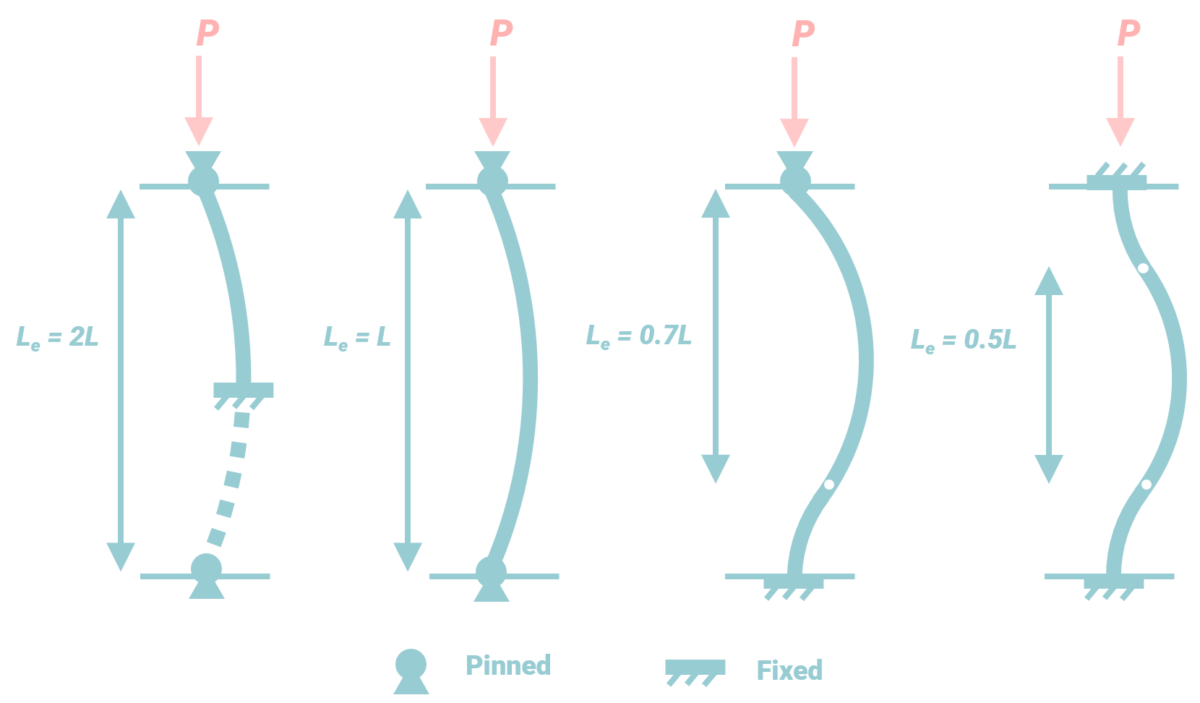
Different end conditions related to column buckling can be identified by the illustrations below:
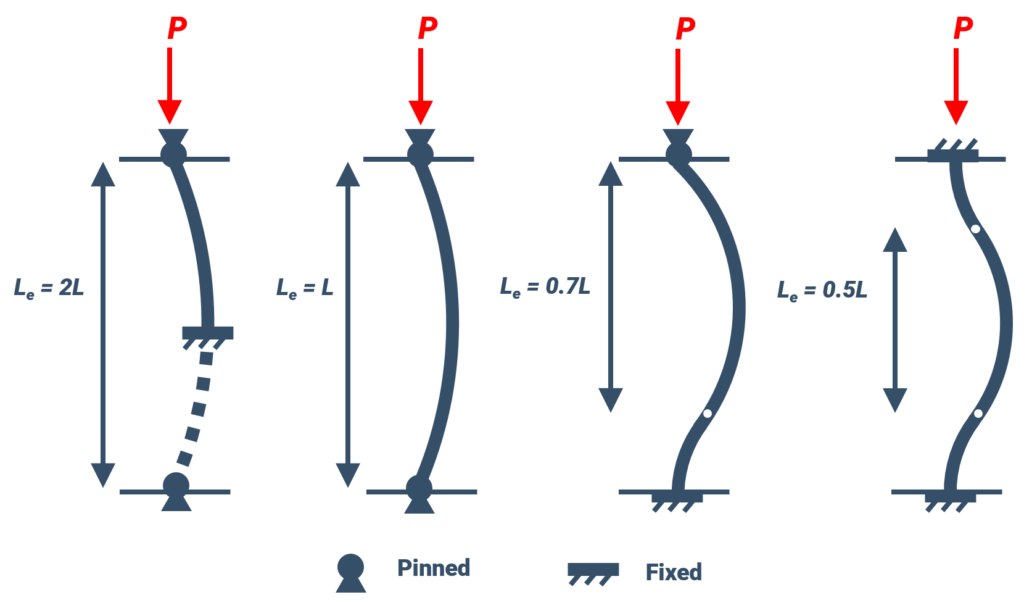
In each of the illustrations different end conditions of columns is demonstrated.
- The first figure shows the end condition with one end fixed and another one free. K for this scenario is 2.
- The second scenario has both ends pinned. K for this scenario is 1.
- The third has one end fixed and the other end pinned. K for this situation is 0.7.
- The fourth is presenting both ends fixed. K for this is 0.65.
K represents the effective length factor which is dependent on the end condition of the column. Each of these illustrations helps in identifying the change in K based on the end condition of the column. The length of the pinned-pinned column is the effective length of the column that is calculated by the following formula;
Leff = K L
Where,
Leff = effective length
L = actual unsupported length
There is an alternative for K, and that is the end coefficient, C. Both of these factors are related to each other inversely that can be shown by the equation below. This equation will help in finding the relationship of C with K.
C = 1/K2
Modes of Buckling
We will discuss different modes of buckling in further discussion in this section.
Flexural-torsional buckling
It is a combination of twisting and bending in response to compression in the column. This mode is therefore common where the column is exposed to bending load.
Crippling
The flange plates in the column section such as channels can bear more load at the corners. Usually, the flanges buckle locally after the extra load is put on them. Crippling is basically the failure of a whole section at once.
Dynamic Buckling
If the column is suddenly loaded and unloaded, it can sustain a higher load. The column can bear less load in case of static load. Usually, this phenomenon occurs in long columns which do not have any support.
Conclusion
Column buckling and relevant factors have been discussed in this blog post. There are different factors that can result in buckling such as increased load. Firstly, the axial compression force is one of the main factors which result in column buckling. Secondly, the elasticity of the material has a high impact.
It is important to note that the compressive strength of the material does not affect the buckling load. On the other hand, the second moment of area of the cross-section is directly proportional to the column buckling load.
A software that can help in calculating column buckling load is Tribby3D. It can help in making designing easier through advanced features. This software is easy to use, convenient and reliable. Read more about the software here and sign up for free at https://tribby3d.com/sign-up